Data Lab实验解答
1. 总体限制要求
注意:Data Lab实验需要用到CSAPP_3th第二章的内容,所以实验之前需要掌握第二章的各种知识。
这个实验中的每个题目都是一个函数,我们要根据规则来实现该函数,并返回正确的答案,每个题会测试很多示例来确定是否符合正确答案。
其中限制要求比较多,以下是实验的限制要求:
1.1 语句限制要求
每个函数中只能含有一个或多个语句,其中所有的语句都不能为以下语句:
- 除了题目所提供的以外,不能使用控制语句。
- 不能定义和使用宏。
- 不能在文件中定义和使用其他的函数。
- 不能使用强制类型转换。
- 不能使用题目所给之外的类型,比如数组,结构体等。
1.2 表达式限制要求
只能包含以下的表达式:
- 对于整型题目来说,只能使用值为0 - 255(
0xff)的整型常量,不能用大的整型常量如0xffffffff;浮点题可以使用。 - 自己定义的局部变量和函数形参,但不能有全局变量。
- 只能包含运算符
=和每一题所给的运算符。
2. 实验题目分析以及解答
本次实验一共13道题,整数题10道,浮点题3道。
2.1 整数有关的题
2.11 实现异或
题目描述
/* * bitXor - x^y using only ~ and & * Example: bitXor(4, 5) = 1 * Legal ops: ~ & * Max ops: 14 * Rating: 1 */ int bitXor(int x, int y) { }
题目分析
这道题让我们只使用位求反~以及位与&这两个运算符来实现位异或^运算符。
我们可以先列出位异或^运算符的真值表:
x |
y |
x^y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
然后根据真值表写出异或表达式的最小项之和:
(~x & y) | (x & ~y)
再用德摩根定律将|替换为~:
~(~(x&~y)&~(~x&y))
这样就得到了异或表达式的实现,所以答案为:
int bitXor(int x, int y) { // 异或表达式的实现 return ~(~(x&~y)&~(~x&y)); }
2.12 实现有符号整数的最小值
题目描述
/* * tmin - return minimum two's complement integer * Legal ops: ! ~ & ^ | + << >> * Max ops: 4 * Rating: 1 */ int tmin(void) { }
题目分析
这一道题就是让我们实现补码整数int型的最小值,我们根据补码的性质以及int所占的位数大小(64位系统就是为32位)就能得到正确答案。
int tmin(void) { // 将1移到最高位 return 0x01 << 31; }

2.13 寻找有符号整数的最大值
题目描述
/* * isTmax - returns 1 if x is the maximum, two's complement number, * and 0 otherwise * Legal ops: ! ~ & ^ | + * Max ops: 10 * Rating: 1 */ int isTmax(int x) { }
题目分析
这一道题让我们寻找到补码整数int型的最大值,并返回1。
我们可以根据异或的性质来比较两个值之间是否相同,也就是:
// 等价于 x == y !(x ^ y)
补码整数int型的最大值0x7fffffff有一个性质,就是2x + 2等于0,除了补码整数int型的-1也有这个性质之外,其他的数都没有这个性质。
因为补码整数int型-1加1可以等于0,所以我们可以通过使用异或~和位与&来判断所给的值是否为-1以及是否2x+2等于0。
所以正确答案为
int isTmax(int x) { // 判断x是否为-1以及2x+2是否为0 return !!(x + 1) & !((x + x + 2) ^ 0); }

2.14 寻找奇数位整数
题目描述
/* * allOddBits - return 1 if all odd-numbered bits in word set to 1 * where bits are numbered from 0 (least significant) to 31 (most significant) * Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1 * Legal ops: ! ~ & ^ | + << >> * Max ops: 12 * Rating: 2 */ int allOddBits(int x) { }
题目分析
这一道题让我们判断,如果一个int的二进制中,所有奇数位都为1,则返回1,否则为0。其中位数从0开始算。
同样,我们可以用异或让x与所有奇数位为1的数进行比较。
正确答案为
int allOddBits(int x) { // all_odd为所有奇数位为1的数 int all_odd = (0xaa << 24) + (0xaa << 16) + (0xaa << 8) + 0xaa; // x与all_odd进行比较 return !((all_odd & x) ^ all_odd); }

2.15 实现相反数
题目描述
/* * negate - return -x * Example: negate(1) = -1. * Legal ops: ! ~ & ^ | + << >> * Max ops: 5 * Rating: 2 */ int negate(int x) { }
题目分析
这一道题让我们不用负号来实现一个数的相反数。
补码整数的相反数实现方法一般是逐位取反,最后再加1,所以我们就可以这样操作。
正确答案为
int negate(int x) { // 逐位取反,再加1 return ~x+1; }

2.16 寻找'数字'
题目描述
/* * isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9') * Example: isAsciiDigit(0x35) = 1. * isAsciiDigit(0x3a) = 0. * isAsciiDigit(0x05) = 0. * Legal ops: ! ~ & ^ | + << >> * Max ops: 15 * Rating: 3 */ int isAsciiDigit(int x) { }
题目分析
这一道题让我们判断一个整数的值是否是表示字符'0'到'9'之间的,如果是,则返回1;否则返回0。
我们通过观察字符'0'到'9'的十六进制式子可以发现:
- 它们的高24位都是相同的,都为
0x0000003X。 - 它们的最低4位中,如果第四位为1,则二三位都会为0,也就是
100X。
根据这两个性质,我们可以通过移位和位与运算符来提取这些位来进行操作,然后用异或进行比较,最后得出结果。
提取位的操作也就是用一个对应所要提取的位为1,其他位为0的数与该数进行位与,所得到的数就包含这些位的信息。
比如:
// 目标串 // 需要提取该串的第16位到24位(从1开始算的位数) int target = 0xaf3849de; // 模式串 // 该串的第16位到24位为1,其他的都为0 int model = 0xff << 16; // 结果 // result的十六进制为0x00380000 int result = target & model;
所以正确答案为
int isAsciiDigit(int x) { // high_four_bits为x的第5位到第8位 int high_four_bits = x >> 4; // low_first_bi为x的第4位 int low_first_bit = x & 0x8; // low_three_bits为x的第2~4位 int low_three_bits = (x >> 1) & 0x7; // 只有第9位到第32位都为0,第5位到第8位为0011,第2~4位为100或者0XX的数才是符号数 return (!(high_four_bits ^ 0x3)) & ((!low_first_bit) | !(low_three_bits ^ 0x4)); } // 另一种解法,使用条件运算 // int isAsciiDigit(int x) // { // int last_x = (x >> 31 & 1); // int last_a = (0x3a >> 31 & 1); // int condition = ~!(last_x ^ last_a) + 1; // int a_me_x = (condition & !((x + ~0x3a + 1) >> 31 & 1)) | ((~condition) & (last_x ^ 1)); // return !((x >> 4) ^ 0x3) & !a_me_x; // }

2.17 实现条件运算
题目描述
/* * conditional - same as x ? y : z * Example: conditional(2,4,5) = 4 * Legal ops: ! ~ & ^ | + << >> * Max ops: 16 * Rating: 3 */ int conditional(int x, int y, int z) { }
题目分析
这一道题让我们只使用位运算相关的运算符来实现条件运算。
因为条件运算是一种分支控制结构,当条件成立执行某表达式,不成立则执行另一表达式。
所以条件运算的构造思路为:
- 我们需要使用某种表达式来控制左右两个子表达式的成立,此时可以用到条件表达式。
也就是条件成立时,一边原样输出,一边全为0;不成立时类似。
此时我们可以想到十六进制串0xffffffff和0x00000000的性质,它们与其他值位与时,一个可以保持值不变,一个将值变为0,并且可以用位取反~来相互转换。 - 根据上面的推理,我们还要连接两个子表达式,并且连接的符号不会影响输出,所以我们可以使用位或
|来连接。 - 接下来要构造条件表达式,使之能够变为
0xffffffff和0x0。
我们可以用逻辑非!来使式子变为0x0。
综上,我们就可以构造出条件运算了。
所以正确答案为
int conditional(int x, int y, int z) { // condition为条件,判断x是否为非0 int condition = ~!!x + 1; // 条件成立输出y,否则输出z return (condition & y) | ((~condition) & z); }

2.18 实现比较
题目描述
/* * isLessOrEqual - if x <= y then return 1, else return 0 * Example: isLessOrEqual(4,5) = 1. * Legal ops: ! ~ & ^ | + << >> * Max ops: 24 * Rating: 3 */ int isLessOrEqual(int x, int y) { }
题目分析
这一道题让我们只使用位运算相关的运算符来实现比较运算符。
因为我们实现的是补码整数的比较运算符,所以有正负数之分。
通过观察数的大小以及正负可得出以下结论:
- 当两个数同号时:
- 当大的数减去小的数时,所得结果都为正数,且都不会溢出。
- 当小的数减去大的数时,所得结果都为负数,且都不会溢出。
- 当两个数异号时:
正数肯定比负数大。
综上,我们需要知道两个数的正负,然后用条件运算进行同异号情况之间的判断。
所以正确答案为
int isLessOrEqual(int x, int y) { // last_x为x的符号位 int last_x = (x >> 31 & 1); // last_y为y的符号位 int last_y = (y >> 31 & 1); // condition为条件,判断是否为同号 int condition = ~!(last_x ^ last_y) + 1; // 同号则判断结果的符号位是否为0;异号则判断y的符号位是否为1 return (condition & !((y + ~x + 1) >> 31 & 1)) | ((~condition) & (last_y ^ 1)); }

2.19 实现逻辑非
题目描述
/* * logicalNeg - implement the ! operator, using all of * the legal operators except ! * Examples: logicalNeg(3) = 0, logicalNeg(0) = 1 * Legal ops: ~ & ^ | + << >> * Max ops: 12 * Rating: 4 */ int logicalNeg(int x) { }
题目分析
这一道题让我们只使用位运算相关的运算符来实现逻辑非运算符。
我们通过观察0和其他非0的数可以发现:
- 对于0来说,它的相反数的最高位总是为0。
- 对于大多数非0的数来说,其相反数的最高位与该数相反;只有补码整数的最小值的相反数与其相同,且最高位都为1。
- 对int型进行右移时,如果最高位为1,则左边添加的位的值为1,否则为0。
根据以上的性质,我们可以考虑将数或者其相反数进行右移,如果右移后的值为0xffffffff,则是为非0的数,如果右移后的值是0,则是0。
所以正确答案为
int logicalNeg(int x) { // 当数为非0时,经过两次移位的结果后都会变为0xffffffff,再加1就为0; // 当数为0时,一直都为0,加1就为1 return ((x | ((~x + 1) >> 31)) >> 31) + 1; }

2.110 查询最少位
题目描述
/* howManyBits - return the minimum number of bits required to represent x in * two's complement * Examples: howManyBits(12) = 5 * howManyBits(298) = 10 * howManyBits(-5) = 4 * howManyBits(0) = 1 * howManyBits(-1) = 1 * howManyBits(0x80000000) = 32 * Legal ops: ! ~ & ^ | + << >> * Max ops: 90 * Rating: 4 */ int howManyBits(int x) { }
题目分析
这一道题让我们通过所给的数,判断该数最少所需要的位数。
我们通过观察整数的二进制可以发现:
- 对于正数来说,我们判断该数所需的最少位的方法为:
从左到右找到该数二进制中的第一个为1的值的位,此位所在的位数(从1开始算)加上符号位(因为是补码整数)就是该数所需的最少位数。 - 对于负数来说,我们判断该数所需的最少位的方法和正数类似,只不过要找到第一个为0的值的位。
根据以上的性质,我们可以考虑使用逐位或者二分法进行查找。
本题的最大可用操作符数量为90,这也证明可以逐位查找,不过因为int有32位,逐位查找太麻烦,所以我们就用二分法进行查找。
进行二分法之前,我们为了方便进行查找,可以将负数的值按位取反,使之也是通过寻找第一个为1的值的位来判断的。
二分法的思路为:
- 每次将所给数的二进制位分为两部分,判断某一部分是否含有值为1的位。
- 如果含有,则所需位数至少为该部分的位数,否则还需进一步判断。
- 然后进入含有值为1的位的那个部分,再次进行查找操作,直至找到第一个为1的值的位或者所给的数没有值为1的位,则就得到了最终的结果。
所以正确答案为
int howManyBits(int x) { // flag为x的符号位 int flag = x >> 31; // 当x为负数,则将其按位取反;否则不变 x = (~flag & x)|(flag & ~x); // 从中间进行二分,并检查左边的部分 int temp = x >> 16; // 条件condition,判断左边是否含有值为1的位 int condition = ~!!temp + 1; // result储存结果,判断有则加上该部分的位数。 int result = condition & 16; // 根据条件condition决定那一部分为含有值的部分,然后进入该部分再此进行查找。 x = (condition & temp) | ((~condition) & x); // 重复以上的部分。 temp = x >> 8; condition = ~!!temp + 1; result += condition & 8; x = (condition & temp) | ((~condition) & x); temp = x >> 4; condition = ~!!temp + 1; result += condition & 4; x = (condition & temp) | ((~condition) & x); temp = x >> 2; condition = ~!!temp + 1; result += condition & 2; x = (condition & temp) | ((~condition) & x); temp = x >> 1; condition = ~!!temp + 1; result += condition & 1; // 最终找到该值,或者所给数不存在值为1的位。 // 不存在,则x为0,否则为1。 x = (condition & temp) | ((~condition) & x); // 最终结果,不要忘记加符号位。 return result + 1 + x; }

2.2 浮点数有关的题
2.21 浮点数乘二
题目描述
/* * floatScale2 - Return bit-level equivalent of expression 2*f for * floating point argument f. * Both the argument and result are passed as unsigned int's, but * they are to be interpreted as the bit-level representation of * single-precision floating point values. * When argument is NaN, return argument * Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while * Max ops: 30 * Rating: 4 */ unsigned floatScale2(unsigned uf) { }
题目分析
这一道题让我们将所给的无符号整数的二进制位当做是float浮点数的二进制位,并对该浮点数乘二,返回乘二后的二进制位。如果该浮点数为无穷或者NAN,则直接返回该值。
我们所用的浮点数标准大部分为IEEE标准754。
该标准对于浮点数与整数的乘积结果,有以下特点:
- 如果浮点数为规格化数:
则对浮点数的乘积就是对阶码编码值的改变。 - 如果浮点数为非规格化数:
则对浮点数的乘积就是对尾数的乘积(也可以看做把尾数整体往左或者右移动)。 - 如果浮点数为特殊值(也就是阶码位全为1):
则对该浮点数进行的乘积对其没有作用。
根据以上的性质,我们可以先提取出浮点数的符号位和阶码位,然后根据阶码编码值进行不同的操作。
所以正确答案为
unsigned floatScale2(unsigned uf) { // 提取符号位 unsigned sign = uf & (1 << 31); // 提取阶码位 unsigned exponent = uf & (0xff << 23); // 当浮点数为特殊值的情况 if (exponent == (0xff << 23)) return(uf); // 当浮点数为非规格化数的情况 else if (exponent == 0) return(sign + uf + uf); // 当浮点数为规格化数的情况 else return(uf + (0x1 << 23)); }

2.22 浮点数转换成有符号整数
题目描述
/* * floatFloat2Int - Return bit-level equivalent of expression (int) f * for floating point argument f. * Argument is passed as unsigned int, but * it is to be interpreted as the bit-level representation of a * single-precision floating point value. * Anything out of range (including NaN and infinity) should return * 0x80000000u. * Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while * Max ops: 30 * Rating: 4 */ int floatFloat2Int(unsigned uf) { }
题目分析
这一道题让我们将所给的无符号整数的二进制位当做是float浮点数的二进制位,并对该浮点数进行类型转换,将其转换成int型整数。如果该浮点数超出了范围(包括为无穷或者NAN),则返回0x80000000u。
对于规格化浮点数转换为整数,我们通常是以以下的流程进行转换的:
- 算出阶码的编码值,并减去偏置值,从左到右按照此值将对应数量的尾数记录下来,这些数就是整数的大部分有效位。
- 再在这些数的最前面加上值为1的位,然后在开头加上多个0,直至已经达到32位。
- 如果符号位为1,则需要将该整数转换为其相反数(按位取反再加1);否则整数的转换就已经完成。
IEEE标准754对于浮点数转换为整数,有以下的特点:
- 如果浮点数的阶码值(进行偏置处理后)小于0或者浮点数为非规格化数时:
则转换后的整数就为0。 - 如果浮点数的阶码值(进行偏置处理后)大于31或者阶码位全为1时:
则转换后的整数就为0x80000000。
根据以上的性质,我们可以先提取出浮点数的符号位、阶码位和尾数位,然后根据阶码值(进行偏置处理后)进行不同的操作。
所以正确答案为
int floatFloat2Int(unsigned uf) { // 提取符号位,并放在末尾 unsigned sign = (uf >> 31) & 1; // 提取阶码位,并放在末尾 unsigned exponent = (uf >> 23) & 0xff; // 提取尾数位 unsigned frac = uf & ((0x7f << 16) + (0xff << 8) + 0xff); // 阶码值(进行偏置处理后) int exponent_val = exponent + ~127 + 1; // 规格化浮点数变为整数的正常转换 int result = (1 << exponent_val) + (frac >> (23 + ~exponent_val + 1)); // 当阶码值(进行偏置处理后)大于31或者阶码位全为1的情况 if (exponent_val > 31) return(0x80000000u); // 当阶码值(进行偏置处理后)小于0小于0或者为非规格化数的情况 else if (exponent_val < 0) return(0); // 当符号位为0的情况 else if (sign ^ 1) return result; // 当符号位为1的情况 else return ~result + 1; }

2.23 2的指数形式的浮点数
题目描述
/* * floatPower2 - Return bit-level equivalent of the expression 2.0^x * (2.0 raised to the power x) for any 32-bit integer x. * * The unsigned value that is returned should have the identical bit * representation as the single-precision floating-point number 2.0^x. * If the result is too small to be represented as a denorm, return * 0. If too large, return +INF. * * Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while * Max ops: 30 * Rating: 4 */ unsigned floatPower2(int x) { }
题目分析
这一道题让我们将所给的补码整数当做以2为底的指数,并将这个2的幂转换为浮点数的形式。
IEEE标准754对于2的幂转换为浮点数,有以下的特点:
- 如果该2次幂的指数在规格化范围内(大于等于-126,小于等于127):
则转换后的浮点数为:- 符号位为0。
- 阶码编码值为偏置值加上该指数。
- 尾数位全为0。
- 如果该2次幂的指数在非规格化范围内(大于等于-149(因为最小的非规格化数为),小于等于-126):
则转换后的浮点数为:- 符号位为0。
- 阶码位全为0。
- 尾数位有且只有一位的值为1的位(当指数为-126时可以没有),该位的编号(从尾数位的最左到右,从1开始计算)为,其余全为0。
- 如果该2次幂的指数大于127,则浮点数为阶码位全为1的特殊值;小于-149时,浮点数为0。
根据以上的性质,我们可以直接根据所给的指数值进行不同的操作。
所以正确答案为
unsigned floatPower2(int x) { // 指数大于127的情况 if (x > 127) return 0xff << 23; // 指数小于-149的情况 else if (x < -149) return 0; // 指数在规格数范围的情况 else if (x >= -126) return (x + 127) << 23; // 指数在非规格数范围的情况 else return 1 << (23 + x + 126); }
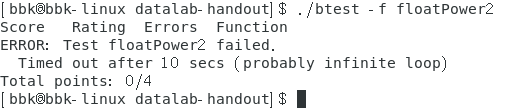
很遗憾,这个题目floatPower2始终无法通过,一直提示死循环。不过不是逻辑上的错误,在VS2019和vscode上完全可以运行,没有进入死循环。所以应该是该实验自带的计分程序的bug。
3. 总结
本次实验中的各个题目的操作符使用情况:
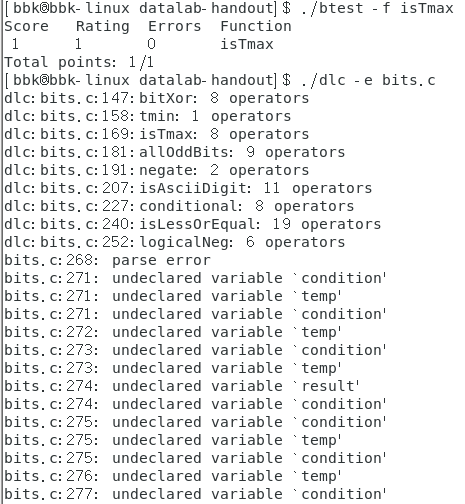
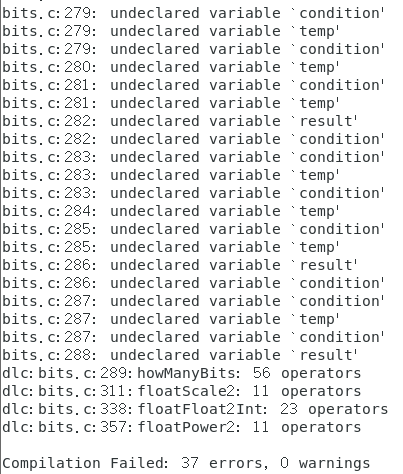
不知道为什么,语法检查程序一直显示howManyBits题中我使用了未声明的变量,但是我明明声明了,而且在VS2019和vscode上完全没有错误,所以应该又是一个该实验自带的语法检查程序中的bug。
本次实验的最终得分:
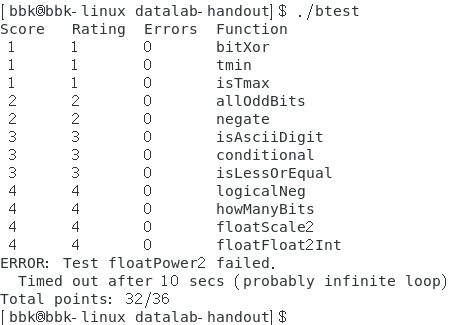
这是我第一次做CSAPP上的实验题,感觉本次实验的题目的难度比较大,加上还有各种语句、表达式和操作符数量的限制,所以整体难度我估计是leetcode上的困难题。
再加上因为都是涉及位运算的,之前刷的题也没有涉及太多这方面的题型,所以花了不少时间。
希望能坚持下来,继续完成后面的实验,加油!